En korrelation är inom statistiken ett samband mellan två oberoende variabler. Det är enklast att mäta korrelation när sambandet är linjärt. Ofta använder man sig av ett sambandsdiagram för att visa att en korrelation föreligger.
Då sprider man ut händelser eller observationer som punkter i ett diagram och sedan drar man en linje för att illustrera sambandet. Korrelationer används och diskuteras inom en mängd olika områden men är främst förknippat med statistik, psykologi och vetenskaplig forskning.
Även inom finansvärlden använder man sig av korrelation, till exempel för att värdera olika investeringar och göra riskanalys.
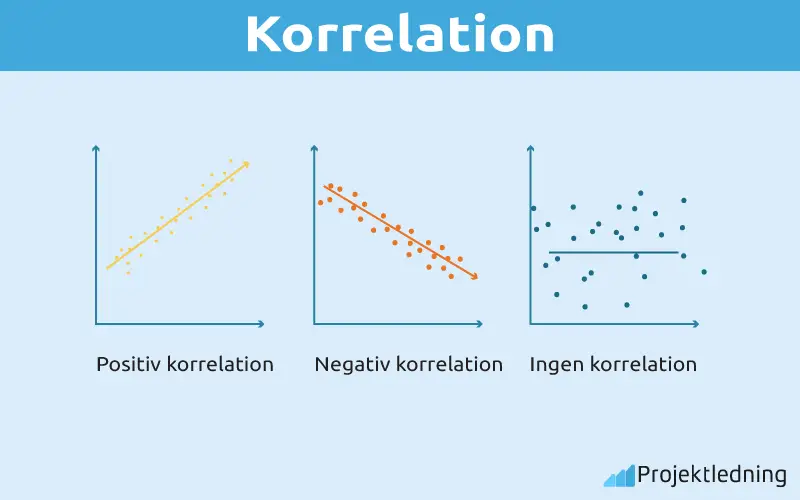
Man använder sig också av korrelationer i vardagen för att förklara hur vissa saker hänger samman och relaterar till varandra. Exempelvis kan man säga att en varas pris och dess efterfrågan är korrelerade. Om priset på varan går upp, går efterfrågan ner, och detta kallas för en negativ korrelation. Man uttrycket korrelationer med bokstaven r och en negativ korrelation uttrycks på detta sätt: -1<r<0.
Ett annat exempel på en korrelation är relationen mellan en persons längd och vikt. När en person blir längre, ökar också oftast dennes vikt. Detta är istället en positiv korrelation eftersom båda variablerna rör sig i samma riktigt och alltså ökar samtidigt. En positiv korrelation uttrycker man på detta sätt: 1>r>0.
Definitionen av korrelation
En korrelation kan man mäta genom att se på två variablers förhållande till varandra. Man ser då hur dessa rör sig och agerar och om mönstret går i samma riktning eller i motsatt riktning. Om variablerna rör sig i samma riktning kallas det en positiv korrelation. Variabler som rör sig i motsatt riktning bedöms istället ha en negativ relation. En perfekt positiv korrelation beskrivs som två variabler som rör sig i exakt samma riktning och samma höjd. När korrelationen är perfekt och positiv är dess värde ett. En perfekt negativ korrelation, som alltså beskriver noll samband, har det exakta värdet noll.
Skillnaden mellan korrelation och kausalitet
Det är mycket vanligt att man blandar ihop korrelation med kausalitet. Korrelation innebär helt enkelt att två variabler har ett samband, men detta innebär inte på något sätt att de har ett orsakssamband. Man bör även ta hänsyn till styrkan av en korrelation. En korrelation utgör alltså ett mått på riktningen och styrkan mellan variabler. En kausalitet innebär istället att det finns ett orsakssamband mellan variablerna, alltså att en av dem har orsakat den andra. En korrelation misstag ofta för att vara en kausalitet och ibland kan människor ta felaktiga beslut på grund av att de misstagit dessa två fenomen. I dessa fall kan det vara så att det finns en tredje variabel man inte räknat med som får ens observerade variabler att verka som att de har ett orsakssamband. Detta kallas ofta för ett skensamband och är mycket vanligare än man tror. I dessa fall kan det vara mycket svårt att identifiera den tredje, okända, variabeln.
Korrelation inom finansvärlden
Inom finansvärlden använder man sig ofta av korrelation för att räkna ut sannolikheten för olika utfall. Detta kan användas av företagare, finansiella analytiker eller investerare. Genom att förstå hur olika aktier rör sig i förhållande till varandra kan man ta mer informerade beslut vid sina investeringar och dessutom göra stora vinster då man identifierar att en historisk korrelation är på väg att ske på marknaden. På många sätt är det detta man menar med att spekulera i aktier. Man gissar på hur ett utfall kommer ser ut, men denna gissning är ofta välgrundad i en korrelationsanalys.
Med hjälp av korrelationer kan man även avgöra potentiella utfall av beslut, och företag kan på detta sätt ta informerade beslut drivna av data. Man kan även använda korrelationer för att analysera historiska korrelationer för att räkna ut hur ett företag kommer att reagera på en viss marknad eller under en viss tid. Detta kan vara mycket användbart då man vill avgöra vad som är en bra tid för exempelvis investering eller produktlansering. Om ett företag haft goda resultat då de lanserat produkter under en viss högtid historisk, kan det vara en god idé att investera en liknande produkt under samma högtid i framtiden. Det finns en mängd olika scenarion inom företagsvärlden där korrelation kan vara mycket användbart som ett analysverktyg.
Prediktiv analys
En av de viktigaste delarna då man använder korrelation är för att beräkna och i förväg skapa sig en bild över risker och möjligheter. Inom företags- och finansvärlden använder man korrelation för att göra prediktiva analyser som kan hjälpa till att förutse framtida händelser. Genom korrelationsanalyser kan man dessutom förutspå framtida trender och få välgrundad data på vad som kommer att bli populärt på marknaden. Detta gör korrelation till ett mycket effektivt sätt att skapa värde för ett företag som vill lansera nya produkter eller tjänster.
Hitta nya affärsmöjligheter
Genom att använda statistiska analysverktyg i form av korrelationsberäkningar kan man hitta nya affärsmöjligheter man kunnat missa annars. Ofta sker beslutsfattande på företag och inom finanssektorn med basis i personliga preferenser eller tankar. Istället för att använda sig av dessa mer ogrundade känslobeslut kan man använda korrelation. På detta sätt kan man hitta möjligheter som annars hade gått förbi obemärkta. Detta är en stor fördel eftersom man i bästa fall hittar en helt oupptäckt marknad och på detta sätt blir ensam om den. Då kan företag eller investerare tjäna stora summor på att göra ett bra, korrelationsbaserat, analysarbete.
Ta bättre beslut
Statistik analys kan hjälpa företagsledare att ta bättre och mer välgrundade beslut eftersom de har en bas av fakta då de presenterar sina idéer. Dessutom skapar detta större förtroende för beslutsfattare eftersom affärsstrategin är grundad i statistisk sannolikhet. Detta innebär att de anställda kan känna större tillit till strategin eller beslutet och därmed känna sig tryggare i processen. Denna typ av förtroende är mycket viktigt då man vill bygga upp ett starkt ledarskap.
Reducera risker och fel
Statistisk analys av korrelation kan vara ett mycket effektivt sätt för företagare och spekulanter inom finansvärlden som vill testa hypoteser och mer riskabla teorier. Detta kan starkt reducera risker och fel eftersom man istället för att behöva göra misstag för att inse att de är just misstag, kan testa sina idéer i förväg. Idag finns en mängd olika dataprogram som gör det enkelt att testa styrkan på sina antagna korrelationer innan man agerar och tar beslut i den riktiga världen.
Korrelationsanalys inom marknadsföring
Ett annat fält där korrelationsanalys har visat sig vara mycket användbart är inom marknadsföring. Detta är föga förvånande eftersom det en korrelationsanalys i praktiken gör är att visa upp att ett samband föreligger och därför kan vara mycket intressant att använda sig av då man vill mäta intresset för en produkt inför utvecklingen eller lanseringen. Dessutom används korrelationsanalys redan febrilt inom psykologin som ett sätt att förstå och mäta beteendemönster. Dessa är självklart mycket intressanta då man vill förstå vad som driver kunder på marknaden. I praktiken skulle detta kunna beskrivas med exemplet att det finns ett samband mellan att vara gravid och köpa babykläder. Denna typ av korrelation är ganska självklar, men det finns också korrelationsanalyser som visar mer dolda korrelationer som kan vara av stort intresse för en hel del företag. Genom att identifiera dessa kan man ligga steget före sina konkurrenter och vara ensam på en marknad andra inte ens vet existerar.
Korrelationsanalys kan alltså skapa en stor konkurrensfördel men man måste samtidigt vara försiktig. Ibland kan korrelationen i själva verket vara en slump och det föreligger i vekligheten inget samband mellan två variabler. Då kan företag investera stora summor i ett marknadsföringsarbete som inte leder någonstans.
Korrelation som forskningsverktyg
Ett fält inom vilket man ofta talar om korrelation är vetenskaplig forskning. Ett forskningsprojekt som använder korrelation som sitt mätverktyg har flera fördelar framför andra sätt att bedriva forskning. Eftersom variablerna mäts oberoende av varandra och utan att man på något sätt behöver ingripa är det ett mycket effektivt verktyg för att utföra observationsstudier.
Fördelar med korrelationsforskning
Det finns en mängd fördelar med att arbeta med korrelation inom forskningsprojekt. Framförallt ger korrelationsbaserad forskning stora möjligheter att observera det som inte kan manipuleras och mätas i labb. Detta gör att man genom observationsstudier kan mäta mer naturliga företeelser och resultatet av forskning bedriven genom korrelation kan därför bli mycket användbar som ett verktyg för att förstå sannolikheten att något skulle kunna hända.
Ingen manipulation av variablerna
En av de största och mest uppenbara fördelarna med att använda sig av korrelation för att förstå samband mellan två variabler i ett forskningsprojekt är att man inte på något vis behöver manipulera variablerna. Hela idén bakom korrelationsforskning är att det utgörs av observationsstudier där data samlas in och sedan mäts och analyseras med hjälp av statistiska dataanalyser. Detta gör att resultatet kan bli mer tillförlitligt och dessutom mer likt verkliga förutsättningar, eftersom man kan göra datainsamlingen i variablernas naturliga miljöer.
Olika metoder för datainsamling möjliga
Det finns två olika metoder man kan använda sig av då man samlar in data i en korrelationsstudie, naturlig observation eller tidigare insamlad data. Detta gör arbetssättet bredare och man har flera olika valmöjligheter då man utför sin studie.
Naturlig observation
Den naturliga observationen bygger på att man studerar sina forskningsobjekt, ofta i deras naturliga miljö, och försöker se till att förutsättningarna är så lika verkligheten som möjligt. Detta gör man för att undvika att datan på något sätt blir manipulerad eller osäker. Det finns en mängd variabler som skulle kunna bete sig annorlunda om de förstod att de var observerade och därför är det ofta mycket viktigt att de naturliga observationerna är diskreta.
Tidigare insamlad data
Man kan även använda sig att tidigare insamlade data från andra studier och implementera dessa i sin egen forskning. Detta är en stor fördel med korrelationsstudier eftersom den typ av data man får ut är väldigt enkel att tolka och använda och därför kan vara relevant även långt in i framtiden. Denna typ av tidigare insamlad data kan analyserad på nya sätt eller användas för att jämföra med nya insamlade data och få ett bredare perspektiv.
Insamlad data och resultat är mer användbara
En stod fördel med korrelationsstudier är just det man kan studera med hjälp av dem. Eftersom det ofta är mer naturliga situationer som studeras kan datan bli mycket användbar och intressant. Det innebär att man kan studera hur människor rör sig inom ett visst område, konsumtionsmönster, åsikter i vissa frågor et cetera. Denna typ av studier kan vara mycket värdefulla för en mängd aktörer och därmed ökar också värdet och användbarheten för dem.
Nackdelar med korrelationsforskning
Samtidigt som det finns en mängd fördelar med detta sätt att bedriva forskning kan man även peka på en hel del saker som gör att det inte fungerar lika bra som andra. Detta handlar främst om att korrelation egentligen inte säger någonting om orsak mellan två variabler och att det ofta tar lång tid att bedriva en korrelationsstudie.
Hittar bara relationer, inte orsak
Korrelation beskriver att två variabler har en relation och alltså på något sätt hör ihop eller relaterar till varandra. Däremot säger det ingenting om att de orsakar varandra. Det innebär att man kan bevisa att när en variabel gör si, gör den andra så, men man kan aldrig svara på frågan ”varför?”. Ofta i forskningssammanhang är det just orsaken man är ute efter, snarare än relationen. Detta kan vara en stor nackdel med korrelationsbaserad forskning.
Korrelationsforskning tar tid
För att få en uppfattning om att en korrelation föreligger behöver man ha en mycket stor mängd data och ofta under en mycket lång tid. Att två entiteter befinner sig på samma plats i ett sambandsdiagram vid en viss tidpunkt kan vara en slump, och för att bevisa att det finns en korrelation mellan dessa behöver man en mängd observationer över tid. Detta kan vara resurskrävande både i form av tid och pengar eftersom det dröjer innan man kan bevisa en direkt korrelation.
Främmande variabler kan påverka resultatet
En stor del av den säkerhet som finns med korrelationsforskning, och som även brukar tillskrivas som en positiv egenskap är att den inte på något sätt behöver manipuleras och att den tillåts ske en naturlig miljö. Detta kan dock samtidigt bidra till att datan som samlas in blir osäker och i värsta fall, felaktig. Denna typ av variabler kan svärta resultatet och få korrelationen att verka starkare eller svagare än den faktiskt är. Ibland upptäcker man dessa främmande variabler, men i vissa fall går de förbi obemärkta och då kan man inte på något sätt ta hänsyn till hur de kan påverkat datan.
Sammanfattning korrelation
Korrelation används alltså inom en mängd olika fält där psykologi, finans, företagsvärlden, statistisk analys och vetenskaplig forskning är några av de vanligaste. Det är dock relativt enkelt att göra beräkningar baserade på korrelation och detta gör det till ett mycket effektivt verktyg även inom en mängd andra områden. Idag finns många dataprogram och system som enkelt kan räkna ut korrelationer och därmed kan man snabbt få tillgång till mycket användbar och värdefull information. På detta sätt kan man få tillgång till analysmaterial som kan göra det enklare att ta välgrundade beslut.
För att skapa en stabil roll på dagens marknad är det viktigt att bygga upp ett förtroende, både till sina investerare och sina anställda. Då kan korrelation vara ett mycket praktiskt verktyg. Om man kan bygga upp sina förslag med starka statistiska bevis kan man övertyga även skeptiker om att en idé kommer att bära. Dessutom kan man använda det som ett verktyg för att analysera och testköra de idéer man känner sig övertygad om men inte säkert vet kommer att fungera. Korrelationsanalys är inom företagsvärlden först och främst ett verktyg för riskanalys, och ett mycket effektivt sådant. Dock kan korrelationer användas för att förbättra ett företag inom en mängd andra områden.
Man kan använda korrelationsanalys för att jämföra olika system man önskar investera i till sitt företag och på detta sätt hitta det mest produktiva och effektiva arbetssättet. På samma sätt kan analyser bidra till stark operationell effektivitet i och med att man kan använda korrelation för att hitta sätt att reducera produktionstider. Med denna typ av analys kan nya arbetssätt växa fram och företag tillåts hitta och implementera mer effektiva arbetssätt. Ett annat mycket effektivt användningsområde för korrelationsanalys är då man vill hitta rotorsaken till ett problem. Om man har ett problem som är återkommande eller som man helt enkelt inte förstår sig på är det mycket viktigt att man lyckas identifiera problemet för att kunna stoppa det från att hända igen. Korrelationsanalys kan vara mycket effektivt för att förstå hur ett problem har uppstått och varför. Det är minst lika viktigt att identifiera negativa faktorer som utgör problem för företag som det är att identifiera positiva faktorer som innebär möjligheter. På dessa och flera sätt kan man använda korrelation för att stärka och säkra sitt företag, sitt projekt eller sin investering.